L’analyse des correspondances multiples (ACM) est une méthode statistique. Elle s’applique à des tableaux généralement de grande taille qui renseignent un ensemble de caractéristiques « qualitatives » pour une population d’individus statistiques (i.e. des individus « biologiques », mais aussi, en certains cas, des institutions, des pays, des collectifs, etc.). Elle extrait de ces tableaux les informations considérées comme les plus importantes, les plus structurantes. La synthèse qu’elle réalise se matérialise par des graphiques où la population étudiée, d’une part, et les caractéristiques renseignées, d’autre part, se distribuent dans des espaces de petite dimension : des droites ou, plus souvent dans les publications, des « plans factoriels ». Sur ces graphiques, les individus statistiques qui se ressemblent (tout comme les modalités partagées par les mêmes individus) sont représentés par des points qui tendent à se regrouper ; la dissemblance produit, au contraire, de la distance.
Cette notice vise à donner un aperçu de cette méthode et des usages dont elle fait l’objet en sciences sociales. Les éléments généraux fournis dans un premier temps éclaircissent des questions (notamment terminologiques) qui peuvent prêter à confusion et fournissent quelques éléments sur les origines et la diffusion de cette méthode, mise au point par des mathématiciens français à partir des années 1960. Dans un deuxième temps, la notice explique dans quelle mesure et en quel sens l’ACM réalise la « synthèse » de l’information contenue dans les tableaux qui lui sont soumis et présente quelques propriétés utiles à la lecture des graphiques qu’elle produit. Pour finir, est évoqué l’usage particulier et très remarqué que Pierre Bourdieu a fait de l’ACM dans le cadre de sa théorie sociale : selon une analogie qu’il a parfois utilisée, les graphiques factoriels pourraient produire des sortes de « cartes géographiques » de ces « espaces théoriques » que sont les champs sociaux1.
Éléments généraux sur la méthode et ses origines
Le terme d’« analyse des correspondances multiples » s’est imposé pour désigner une technique de la statistique multivariée qui vit le jour dans les années 1960 et 1970 mais peut être considérée comme une extension d’une technique plus ancienne et plus connue : l’analyse en composantes principales (ACP). L’ACP permet de synthétiser par une série de « facteurs » un tableau renseignant des variables numériques pour une population d’individus. Elle est utilisée au moins depuis les années 1940, notamment en psychologie. L’ACP a par exemple pu être mobilisée par des psychologues qui, tout en appréhendant « l’intelligence » comme une faculté multidimensionnelle, cherchaient à déterminer, par-delà la diversité des composantes qu’ils mesuraient par des tests (intelligence conceptuelle, pratique, affective, etc.), un facteur principal à l’image du « quotient intellectuel ».
L’ACM traite, elle, de variables « qualitatives » ou « catégorisées », ce qui la rend particulièrement intéressante en sciences sociales. La catégorie socio-professionnelle, l’appartenance religieuse ou le sexe, par exemple, impliquent en effet des opérations de catégorisation : chaque individu se voit assigné à une et une seule catégorie, les catégories étant par ailleurs en nombre fini, et si l’on peut repérer, dans une population donnée, une catégorie « modale » plus fréquente que les autres, il n’est pas possible de calculer de « moyenne ».
Si les termes d’« analyse en composantes principales » et d’« analyse des correspondances multiples » sont aujourd’hui de rigueur, un flou terminologique existe dans la littérature, surtout la plus ancienne. L’expression d’« analyse factorielle » a été très utilisée au sujet de l’ACP et, par extension, de toutes les techniques qui, comme l’ACM, extraient des « facteurs ». Le terme d’« analyse factorielle des correspondances » (AFC) a aussi été beaucoup employé en français à partir des années 1970. À l’origine, il désigne ce qu’on appelle plus volontiers aujourd’hui « l’analyse des correspondances standard »2. Celle-ci s’applique à des tableaux croisant, comme le fait une « table de mobilité », deux variables qualitatives. Elle ressemble beaucoup au test bien connu du « chi-2 ». Historiquement, et mathématiquement, l’AFC est un intermédiaire entre l’ACP et l’ACM. Permettant d’étudier la relation entre deux variables, elle représente une extension de l’ACP conçue comme méthode d’analyse des corrélations, mais elle ouvre la voie au traitement de variables qualitatives.
Jozef Krakovsky, À la recherche du paysage (2008)
L’AFC puis l’ACM connaissent leurs développements majeurs en France à partir des années 1960 sous l’impulsion de l’« école française d’analyse des données » réunie autour du mathématicien Jean-Paul Benzecri. La mise au point de l’ACM – et l’invention du terme d’« analyse des correspondances multiples » – est le fait de ce groupe qui se constitue dans une époque où l’informatique progresse rapidement (et son apport tiendra aussi à la création de programmes permettant de mettre en œuvre « l’analyse des données »). Entre autres choses, Benzecri entend tirer profit des nouvelles possibilités techniques : avec les ordinateurs des années 1960, il devient possible de traiter des « ensembles immenses de données, naguères vouées au feu ou à la poussière »3 par des calculs inenvisageables auparavant, comme la diagonalisation de grandes matrices carrées symétriques qu’implique les techniques d’« analyse des données ». Pour Benzecri, les progrès de l’informatique sont l’occasion à saisir pour refonder la pratique des statistiques, notamment en sciences humaines. L’« analyse des données » lui paraît notamment préférable aux analyses rituelles de tableaux croisés parce que, plutôt que d’étudier les relations statistiques entre des variables prises deux par deux (en y projetant, de façon souvent hasardeuse, des relations de causalité), elle les inscrit dans des réseaux de relations beaucoup plus vastes4.
Benzecri conteste les conceptions statistiques dominantes à l’époque (comme aujourd’hui) aux États-Unis et à l’échelle internationale, qui ont partie liée avec un cadre probabiliste, une ambition modélisatrice et, partant, avec un grand nombre d’hypothèses a priori. Rappelant que « statistique n’est pas probabilité », il moque les statisticiens qui « ont édifié une pompeuse discipline, riche en hypothèses qui ne sont jamais satisfaites dans la pratique »5. Il critique la prolifération des « modèles, forgés a priori puis confrontés aux données par ce qu’on appelle des ‘tests’ » : pour lui, « le modèle doit suivre les données, non l’inverse »6. Il juge l’importation dans la pratique statistique d’un raisonnement expérimental souvent inadéquat en sciences humaines, compte tenu des difficultés qu’y rencontre l’expérimentation.
L’analyse des données se fonde sur des principes différents. Elle oppose au probabilisme l’algèbre et la géométrie ; son ambition centrale consiste, plutôt qu’à tester des modèles posés a priori, à déterminer les principes structurants de jeux de données sur la base d’une « analyse sans a priori (il faudrait dire la synthèse), de données multidimensionnelles »7. Il ne s’agit pas, pour Benzecri, de récuser toute visée modélisatrice ou de renoncer à l’établissement d’une « hiérarchie de causes », mais de poser comme préalable indispensable la recherche des « axes [suivant lesquels] se rangent les masses »8. Puisque « la science doit aborder un ensemble aussi vaste que possible de faits, même imparfaitement décrits, et, par la synthèse, trouver systématiquement les gradations et les oppositions véritables », les « méthodes multidimensionnelles » doivent jouer le rôle central ordinairement imparti aux modèles probabilistes ou aux « études unidimensionnelles »9. De toutes les « méthodes multidimensionnelles » qui composent l’« analyse des données », les variantes de « l’analyse factorielle » sont les plus importantes, les méthodes de classification (qui répartissent une population statistique, non pas dans un espace continu, mais dans des classes) devant être perçues comme « auxiliaire[s] »10.

Jozef Krakovsky, Peinture secrète (2008)
L’« école française d’analyse des données » est très dynamique dès le milieu des années 1960. Elle comporte, à la Faculté des sciences de l’Université de Paris, un volet pédagogique important11 et, à la fin de la décennie, de jeunes statisticiens formés à ces nouvelles méthodes les introduisent dans les organismes statistiques français où ils sont recrutés. Toutefois, ni Benzecri ni ses collaborateurs n’enseignent à l’École nationale de la statistique et de l’administration économique (ENSAE), école d’application de l’INSEE. L’INSEE, par ailleurs, commence alors à se convertir à l’économétrie d’origine anglo-saxonne. Pourtant, l’« analyse des données » y trouve tout de même des relais, notamment auprès de jeunes administrateurs sensibles à l’alternative qu’elle représente dans un univers statistique dominé par les normes venues des États-Unis12. L’un d’entre eux, Michel Volle, introduit un enseignement d’« analyse des données » à l’ENSAE dès 1973 et publie un ouvrage sur la méthode en 1978 qui connaît un succès tel qu’il est réédité dès 198113.
Ces jeunes statisticiens, et particulièrement ceux qui travaillent dans des organismes en relation avec les sciences humaines, jouent un rôle important dans la diffusion de l’« analyse des données ». On peut citer Ludovic Lebart qui, auteur d’un manuel plusieurs fois réédité à destination de chercheurs et étudiants en sciences humaines14, travaille auprès de Benzecri et est passé, dans les années 1970, par le CREDOC, organisme où plusieurs chercheurs (dont Nicole Tabard) pratiquent alors intensément « l’analyse des données ». Ces statisticiens assistent souvent les sociologues adoptant les nouvelles techniques. Dans la Revue française de sociologie, c’est en 1970 que paraît un premier article utilisant une « analyse factorielle des correspondances », dans le cadre d’une enquête dans une galerie de reproductions de tableaux15. En 1972 et en 1975, un article de sociologie de l’éducation et un autre sur le patrimoine des agriculteurs recourent à leur tour à l’AFC16. Au milieu des années 1970, Pierre Bourdieu et les sociologues qui travaillent avec lui commencent à pratiquer l’analyse des correspondances. À partir de 1976, des analyses des correspondances sont assez régulièrement publiées dans la revue qu’ils viennent de créer, Actes de la recherche en sciences sociales. La simple consultation du site Persée montre que le phénomène n’est pas propre à la sociologie : dans les années 1970 le vocable d’« analyse factorielle » se diffuse (et bien souvent apparaît) dans des revues de géographie, de démographie, d’études rurales et, à un moindre degré, d’histoire et de science politique.
En France, l’AFC et l’ACM sont devenues des méthodes que connaissent, même lorsqu’ils ne la pratiquent pas, la plupart des chercheurs en sciences humaines recourant à des outils statistiques. À partir des années 1980, si l’effet de mode et de nouveauté s’émousse un peu, elles restent régulièrement utilisées dans des revues de sciences humaines. Les progrès de l’informatique, puis à partir des années 1990 et surtout 2000, la multiplication et la diffusion des logiciels stimulent même leur diffusion. Elles sont certes davantage concurrencées par l’importation plus intense de méthodes très pratiquées dans le monde anglo-saxon, souvent associées à la conception de la statistique que Benzecri rejetait. À l’INSEE en particulier, dès les années 1980, « l’analyse des données » régresse (de façon très visible, dans Économie et Statistique) au profit de méthodes de modélisation plus « internationales ». Le phénomène se produit aussi en sociologie, mais de façon plus tardive et moins prononcée ; des formes d’éclectisme associant l’analyse des données et des modèles reposant sur des analyses de régression y voient même le jour.
L’ACM reste cependant peu connue hors de la France et de quelques autres pays européens. Le refus de Benzecri d’aller défendre ses idées et ses méthodes dans le monde anglo-saxon a sans doute joué un rôle17. Certains de ses collaborateurs ou, dans les années 1980, Michael Greenacre, un chercheur qui travaille en Espagne, entreprennent bien de vulgariser l’AFC et l’ACM auprès de chercheurs en sciences humaines anglophones, tandis que les méthodes françaises d’« analyse des données » intègrent les principaux logiciels statistiques, mais l’analyse des correspondances se diffuse assez peu en sociologie ; à de très rares (et de surcroît assez anecdotiques) exceptions près18, elle n’a, à ce jour, quasiment jamais été évoquée, débattue ou pratiquée dans une revue comme l’American Journal of Sociology. Une évolution s’observe pourtant sur ce point depuis la fin des années 1990, souvent liée au travail de vulgarisation opéré par Henry Rouanet et Brigitte Le Roux. Ils publient notamment, en 2004, Geometric Data Analysis chez Kluwer puis, en 2010, un volume spécifiquement consacré à l’ACM chez Sage dans une collection, « Quantitative Applications in the Social Sciences », disposant d’un crédit particulier chez les « quantitativistes » anglo-saxons19. La diffusion internationale des travaux de Pierre Bourdieu joue également un rôle. La tentation de reproduire les opérations empiriques auxquelles celui-ci procédait, particulièrement dans La Distinction, est, à partir des années 2000 surtout, à l’origine d’une série de travaux qui donnent lieu, hors de France, à des publications recourant à l’ACM20. En sociologie de la culture, au moins, la pratique de l’ACM cesse clairement d’être une spécificité française à partir de la deuxième moitié des années 2000 dans des revues européennes anglophones comme Poetics ou Cultural Sociology21.
Quelques propriétés géométriques de l’ACM
Après ces éléments généraux sur l’analyse des données, il est possible de rassembler quelques éléments aidant à comprendre comment les graphiques d’une ACM sont produits et comment ils doivent être lus. Il s’agit d’éclairer la « boîte noire » de « l’analyse des données » au travers de laquelle « un ensemble de données en entrée » se transforme en « une représentation visuelle en sortie »22.
Mathématiquement, les techniques d’« analyse factorielle » (ACP, AFC ou ACM) reposent sur des opérations algébriques assez abstraites. L’adoption d’une vision géométrique a le mérite d’être assez intuitive23. Si, réalisant une analyse factorielle sur un logiciel statistique, on a l’impression de soumettre à ce dernier un tableau et d’obtenir, « en sortie », une représentation visuelle, l’apport de la méthode consiste en fait à donner une représentation partielle dans des espaces de petite dimension (souvent, un « plan factoriel ») d’un « objet » qui est équivalent au tableau mais qui, la plupart du temps, ne peut être représenté que dans un espace comportant un nombre de dimensions beaucoup plus important. Présentée de cette manière, la transformation qu’opère l’analyse factorielle diffère peu du problème auquel se heurte le dessin ou la photographie (c’est-à-dire des représentations sur des espaces en deux dimensions) d’un volume.
Photographier un objet de la vie quotidienne en trois dimensions, oblige à adopter un point de vue parmi de nombreux points de vue possibles qui ne se valent pas. Les devinettes reposant sur des dessins très simplifiés (les « droodles »), rappellent parfois de façon amusante que certains points de vue rendent l’objet représenté méconnaissable : représenté à la verticale, un homme portant un sombrero peut se réduire à deux cercles concentriques. Pour rendre un objet reconnaissable, certains points de vue paraissent privilégiés. Un site Internet prodiguant des conseils pour photographier des œuvres d’arts recommande ainsi que « le plan du film [soit] parfaitement parallèle au plan de l’œuvre à photographier [et] l’objet […] parfaitement centré dans le cadre »24. L’analyse factorielle procède selon un principe comparable et les statisticiens disant parfois qu’elle opère comme nous le faisons « spontanément » lorsque, pour suggérer un chameau par un dessin rapide, nous le représentons de profil : c’est la meilleure façon de restituer son « volume » (le chameau est grand et long, mais il est mince) et sa spécificité (un dessin de face ne permettrait plus de distinguer ses deux bosses). Ce faisant, nous choisissons, outre de placer le chameau au centre du dessin, de le représenter selon deux axes qui nous paraissent les meilleurs.
Pour se convaincre que l’analyse factorielle procède ainsi, on peut se placer dans le cas très simple d’une ACP sur deux variables quantitatives. Le tableau 1 renseigne ainsi pour les catégories socio-professionnelles de l’INSEE deux grandeurs numériques : le taux de propriétaires ou d’accédants à la propriété et la proportion de membres de la catégorie qui déclarant être allés au théâtre au cours des 12 derniers mois. Deux indicateurs statistiques figurent au bas de chaque colonne : la moyenne (non pondérée) de la variable et sa variance qui informe sur sa plus ou moins grande dispersion. Le fait que la variance soit plus élevée dans la deuxième colonne renvoie au fait que les écarts entre les catégories sont manifestement plus importants pour la fréquentation du théâtre (quasiment nul dans certaines catégories, le taux monte au-delà de 50 % dans d’autres) que pour le taux de propriétaires (celui-ci est presque toujours compris entre 40 % et 70 %).
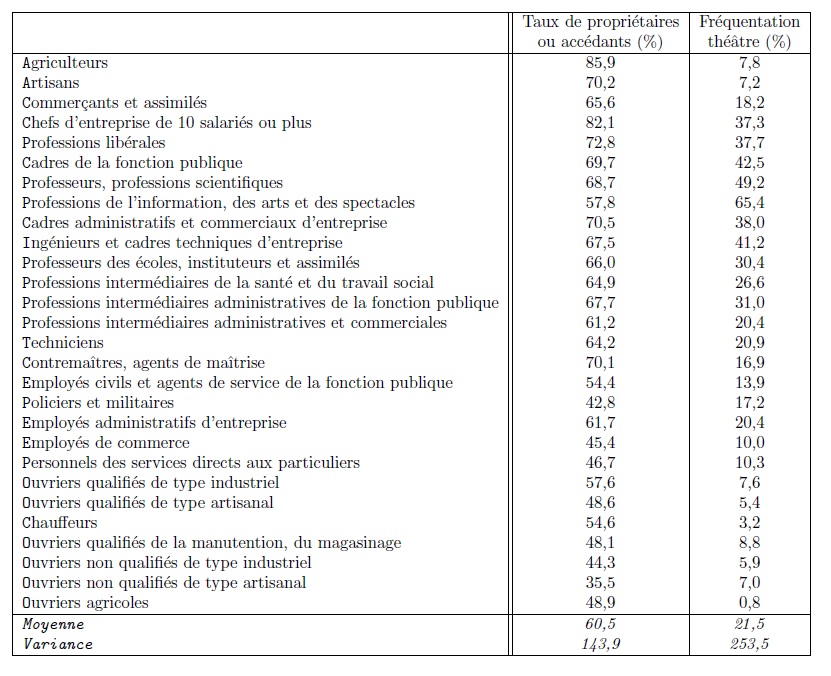
Tableau 1. Le lien entre la propriété immobilière et la fréquentation des théâtres
Le tableau 1 est équivalent à un graphique où l’axe horizontal correspond à une variable (sur le graphique 2, le taux de propriétaires) et l’axe horizontal à la seconde. Sur ce graphique, l’ensemble des catégories socio-professionnelles sont représentées par un nuage de points. Le barycentre G du nuage a pour coordonnées les taux moyens observés dans les différentes catégories (par conséquent 60,5 sur l’axe horizontal et 21,5 sur l’axe vertical). La dispersion ou variance du nuage peut être calculée : elle vaut 397,3, soit, à l’arrondi près, la somme des variances de chacune des deux variables (143,9+253,5=397,4).
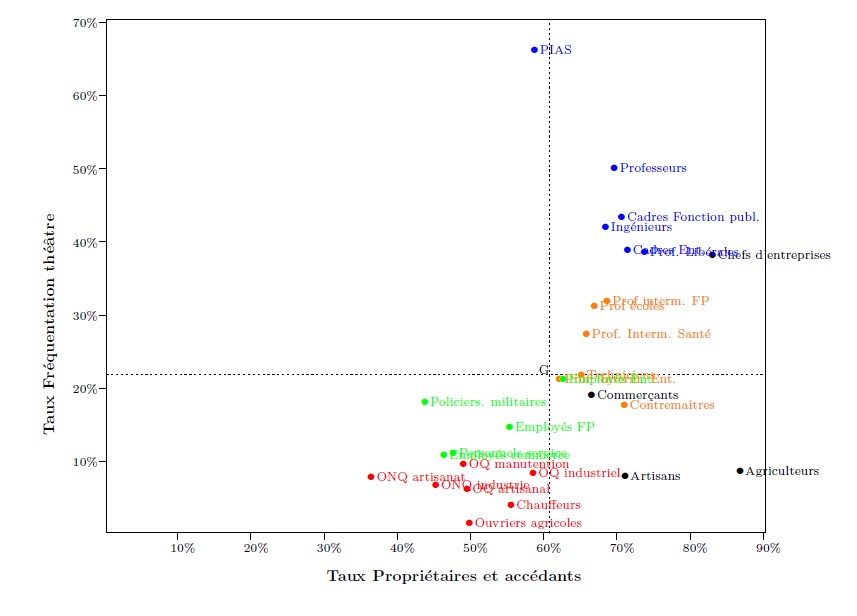
Graphique 1. Le nuage des individus
Un premier changement, simple à opérer, consiste à centrer l’objet, c’est-à-dire à faire de G le centre du repère. Les coordonnées des points sur les axes sont alors celles qui figurent dans le tableau 2 : ce sont les écarts à la moyenne. La valeur indiquée pour le taux de propriétaires chez les agriculteurs par exemple n’est plus de 85,9 %, mais de 85,9-60,5=25,4 points. Elle devient une information qui renseigne sur la position de la catégorie par rapport à l’ensemble de la population. Le graphique 2, comme le tableau 2, invite à considérer des différences. Le nuage a la même forme et la même orientation sur les graphiques 1 et 2, les axes ont les mêmes directions, ils n’ont fait l’objet que d’une translation.
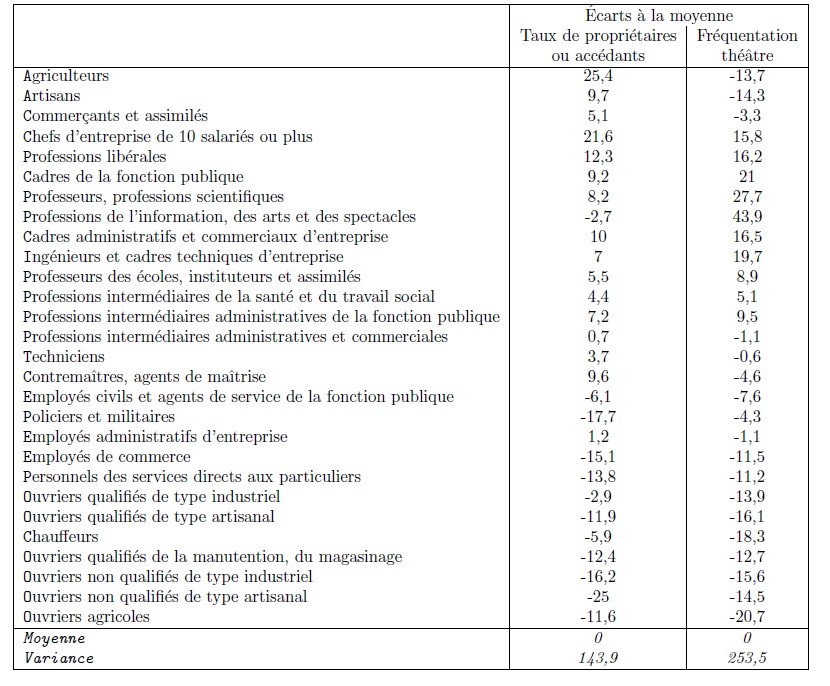
Tableau 2. La relation entre le statut de propriétaire et la fréquentation des théâtres
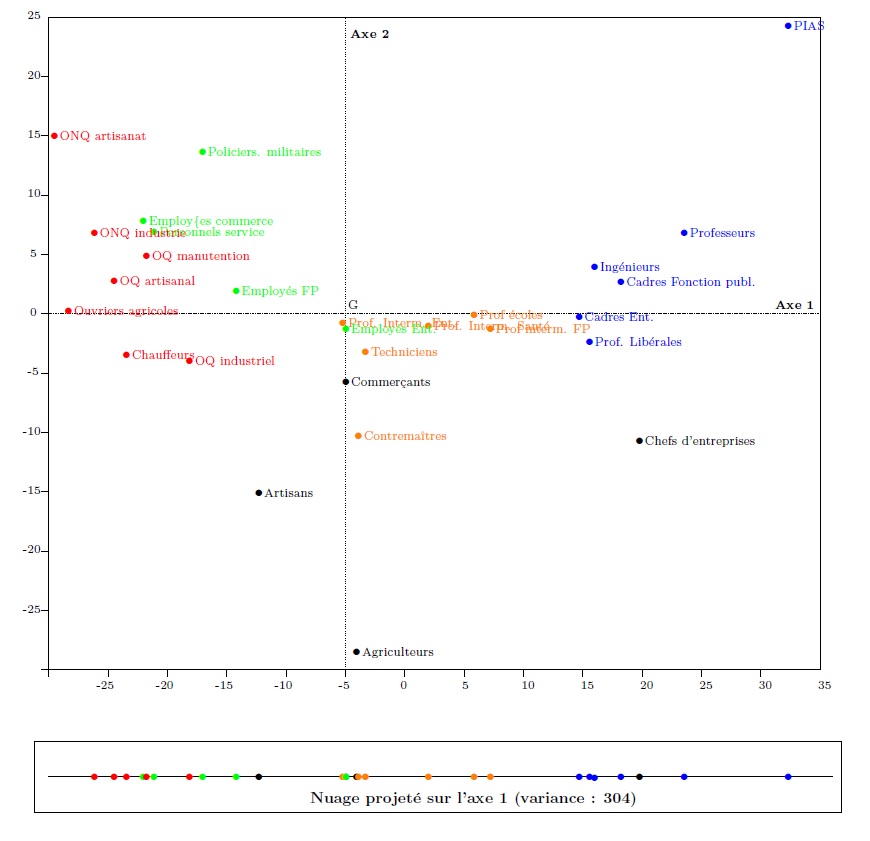
Graphique 2. Le nuage centré des individus
Il est indifférent de soumettre le tableau 1 ou le tableau 2 à une ACP. Dans les deux cas, un logiciel produit « en sortie » les deux graphiques suivants :
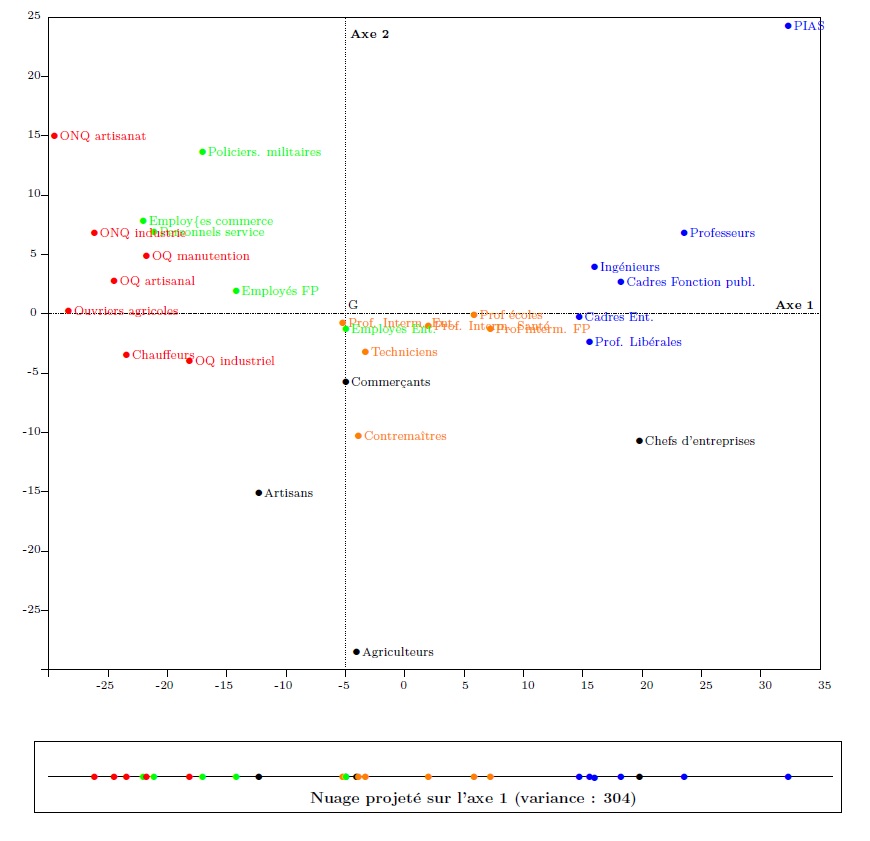
Graphique 3. Les individus dans le plan factoriel
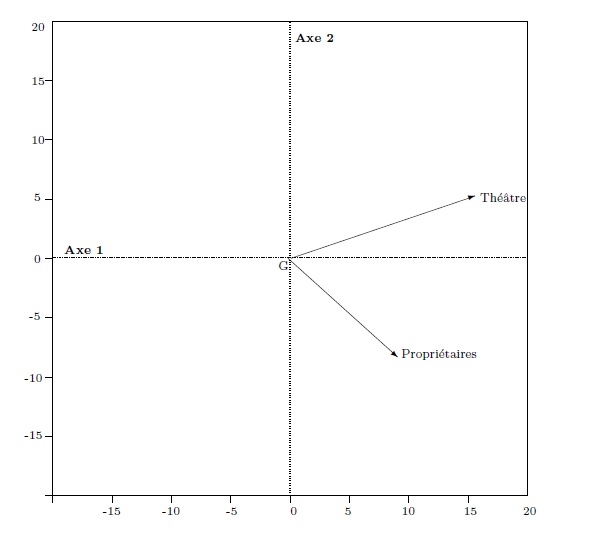
Graphique 4. Les variables dans le plan factoriel
Il apparaît que le graphique 3 (« en sortie ») ne diffère du graphique 2 (« en entrée ») que par un changement de repères qui a bien sûr conservé la forme du nuage mais qui a modifié son orientation ainsi que la direction des axes. On passe du graphique 2 au graphique 3 par une simple rotation autour de G (voir animation).
Animation 1.
Une particularité du nouveau repère est cependant que ses axes sont en quelque sorte ordonnés : ils ont été déterminés de manière à ce que la projection du nuage de points sur l’axe horizontal soit la « meilleure » représentation possible du nuage sur une droite (c’est-à-dire dans un espace à une dimension).
Le nuage du graphique 3 peut en effet être projeté (orthogonalement) sur toutes les droites du plan. Si sur le graphique 2, le nuage est projeté sur la droite horizontale (voir le cartouche au bas du graphique 5), on obtient un nuage de points alignés, chaque point ayant pour coordonnée le taux de propriétaires dans la CSP à laquelle il correspond. Ce nuage a la variance du taux de propriétaires : 143,9.
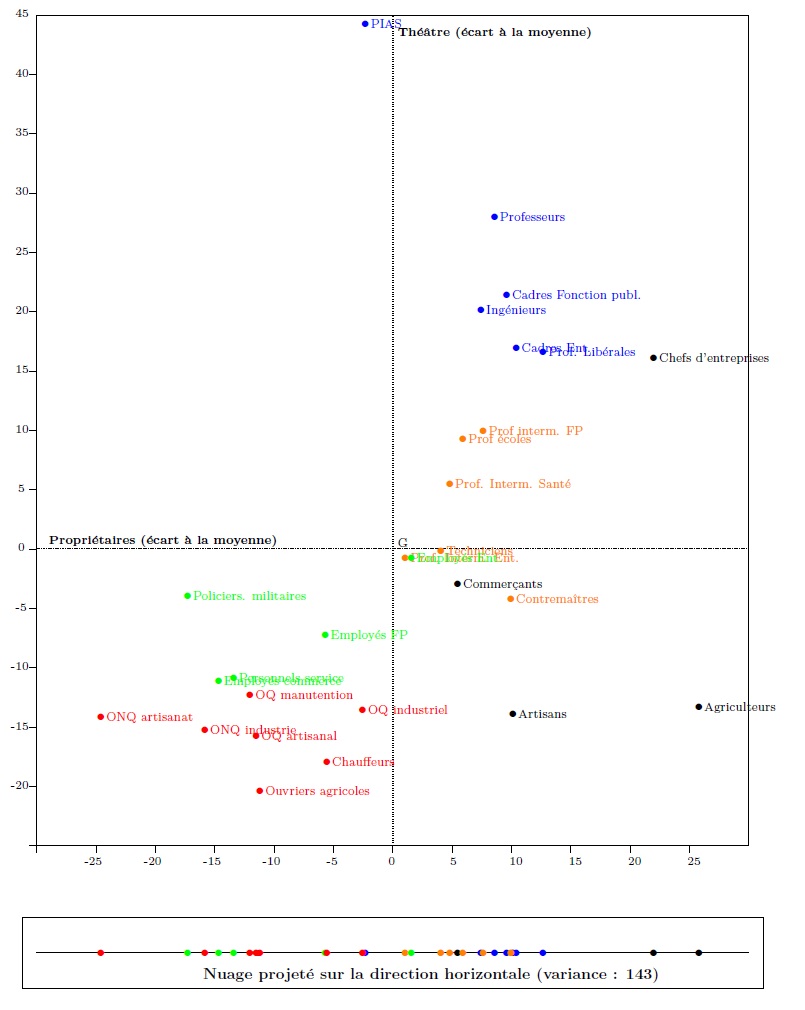
Graphique 5. La projection sur la droite horizontale
Le nuage du graphique 2 peut être projeté sur une droite faisant un angle de 5° avec l’horizontale. Le nuage projeté sur cette droite (graphique 6) est légèrement plus dispersé que ne l’était le nuage projeté sur la direction horizontale : sa variance est d’environ 160.
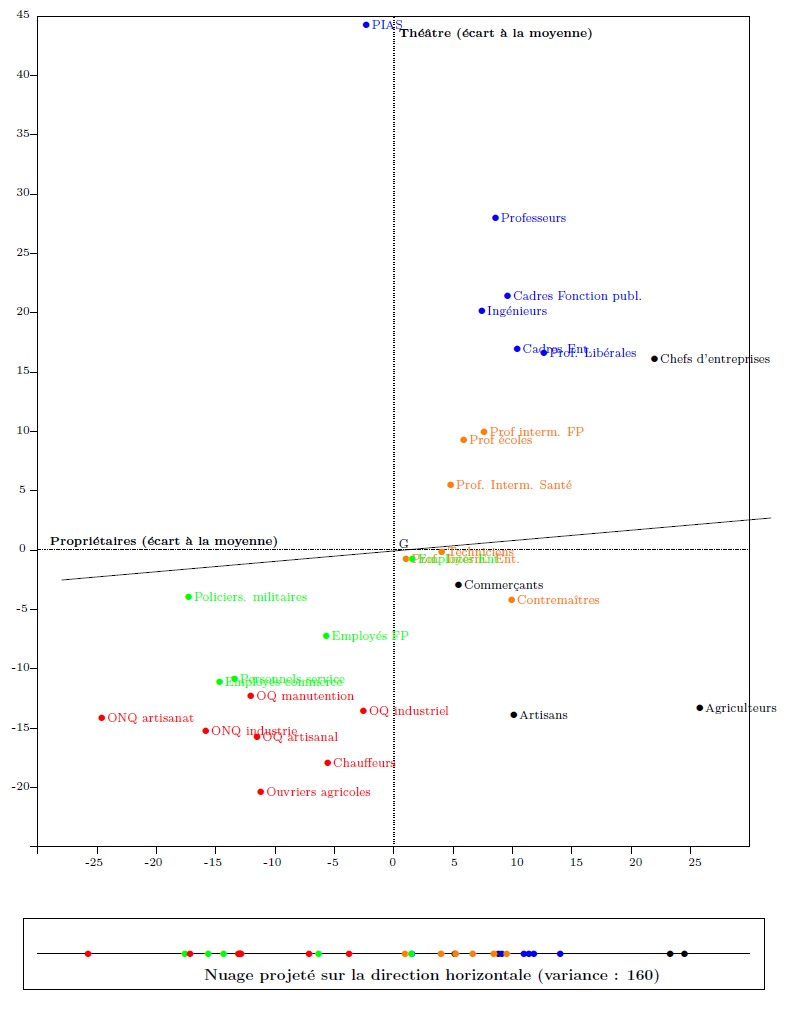
Graphique 6. La projection sur la droite faisant un angle de 5° avec l’horizontale
La même opération peut être reproduite pour des droites de plus en plus inclinées, jusqu’à la droite qui, faisant un angle de 180°, ramène à la direction horizontale. Lors de ces projections successives (graphique 7), la variance du nuage projeté croît dans un premier temps (jusque vers 61°), puis le mouvement s’inverse avant de réaugmenter (au-delà de 150°) sans jamais réatteindre néanmoins le maximum observé aux alentours de 60,58°.
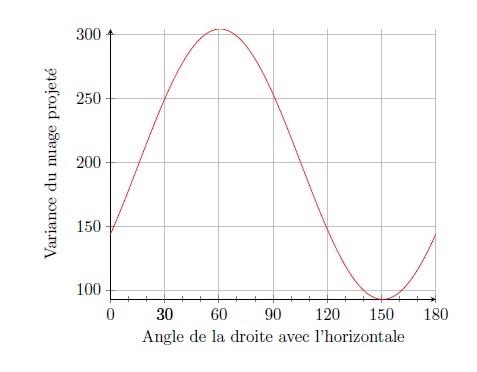
Graphique 7. La variation de la dispersion du nuage projeté en fonction de l’angle d’inclinaison de la droite
Dans une ACP, cette droite, sur laquelle la variance du nuage projeté culmine, constitue le « premier axe ». La variance du nuage projeté sur cet axe est la « valeur propre » de l’axe : elle vaut ici 304, soit 304,7/397,4≈76,6 % de la variance du nuage du graphique 2. Définie de façon plus intuitive, cette droite est la « direction principale » du nuage : c’est à peu près celle que l’on tracerait sur le graphique 2 s’il fallait suggérer l’orientation générale du nuage (à l’évidence, il s’étend grossièrement depuis le Sud-Ouest vers le Nord-Est). Maximisant la dispersion du nuage projeté, cette droite maximise les différences entre les individus statistiques étudiés. Projeter le nuage du graphique 2 sur cette « droite d’étirement maximum », c’est faire en sorte que les catégories les plus éloignées sur le graphique 2, c’est-à-dire les plus dissemblables (au regard des deux indicateurs considérés simultanément), soient aussi éloignées que possible sur cette projection en une dimension. Pour dire les choses encore autrement, le premier axe exprime l’opposition principale entre les catégories socio-professionnelle sous le rapport des deux variables retenues. Il est une sorte d’indicateur unidimensionnel qui synthétise les différences relatives aux deux indicateurs.
Jozef Krakovsky, Mon premier vélo (2008)
À une extrémité de l’axe, se regroupent les catégories qui présentaient, dans le tableau 2, des écarts à la moyenne importants et négatifs pour les deux variables étudiées : toutes les sous-catégories ouvrières en particulier. Les catégories situées à l’autre extrémité, les chefs d’entreprise et les « cadres et professions intellectuelles supérieures » ont la caractéristique inverse (y compris, en un sens, les professions de l’information et des cadres : l’axe opérant une synthèse, leur fréquentation du théâtre particulièrement élevée « compense » leur taux de propriétaires, proche de la moyenne observée toutes catégories confondues). De la gauche à la droite de l’axe, des ouvriers aux cadres, les deux variables tendent à augmenter : c’est ce qu’exprime le deuxième graphique issu de l’ACP ; les vecteurs représentant les variables sont orientés vers l’Est, c’est-à-dire la direction des cadres.
Une ACP ne détermine pas seulement la droite principale, mais un nouveau repère orthogonal qui comporte autant d’axes que le repère initial (ou encore autant de variables que le tableau de départ). Dans le cas présent, un second axe est donc déterminé : c’est la perpendiculaire au premier axe passant par G. Ce deuxième axe renvoie à une opposition secondaire entre les catégories qui s’écartent du profil moyen positivement pour l’une des variables, mais négativement pour l’autre. Comme le tableau soumis à l’ACP est ici en deux dimensions, ce deuxième axe est aussi le dernier et le « premier plan factoriel », constitué du premier et du deuxième axe, restitue toute l’information contenue dans le tableau.
Si le tableau comportait, non plus 2 mais n variables, il faudrait imaginer une procédure identique : le nuage de points représenté ici sur les graphiques 1 et 2 se déploierait dans un espace à n dimensions. L’ACP déterminerait sa direction principale, puis (n-1) autres axes perpendiculaires les uns aux autres, le ie axe étant, parmi toutes les droites passant par G et perpendiculaires au (i-1) premiers axes, celle sur laquelle la variance du nuage projeté est maximale.

Jozef Krakovsky, 143-10 (2010)
La compréhension de l’ACM suppose un effort d’abstraction supplémentaire. Comme la présence de variables qualitatives ne peut permettre (même dans un espace comportant un nombre de dimensions suffisant) une représentation équivalente au graphique 2, un artifice est utilisé : chaque variable est transformée en autant de « variables indicatrices » qu’elle comporte de modalités ; la variable indicatrice prend la valeur 1 si l’individu se rattache à la modalité, 0 dans le cas contraire. De cette manière, la population étudiée pourrait être représentée par un nuage de points dans un espace comportant autant de dimensions qu’il y aurait au total de modalités.
On peut prendre l’exemple d’un tableau assez simple (mais assez pauvre en termes sociologiques) qui renseigne, pour les membres du gouvernement français en fonction en janvier 2016 cinq variables : le sexe (2 modalités : homme/femme), la tranche d’âge (3 modalités : moins de 45 ans/45-60 ans/plus de 60 ans), un indicateur relatif au diplôme (3 modalités : ENA/doctorat, IEP ou autre grande école/formation universitaire), un autre relatif à leur déclaration de patrimoine (3 modalités : patrimoine déclaré inférieur à 200 000 € ; compris entre 200 000 € et 1 million d’euros ; supérieur à 1 million d’euros) ; un dernier relatif aux citations dont chaque ministre avait chacun fait l’objet dans Le Monde avant l’élection de François Hollande comme président de la République (3 modalités : moins de 20 citations ; de 20 à 100 citations ; plus de 100 citations), etc. Le tableau 3 indique les premières lignes du tableau (pour les cinq premiers ministres par ordre alphabétique).
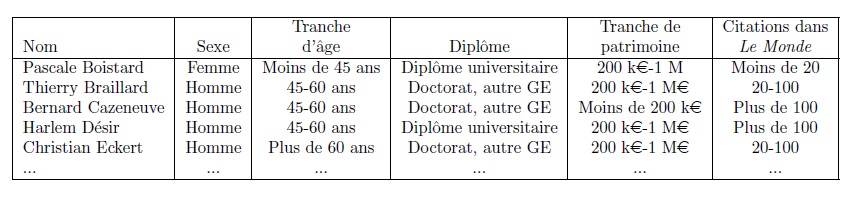
Tableau 3. L'extrait du tableau sur les membres du gouvernement
Dans son intégralité, le tableau comporte 33 lignes, une par ministre. Puisqu’il est composé d’une variable à deux modalités et de quatre variables à trois modalités, il faut s’imaginer qu’un nuage des individus pourrait être représenté dans un espace de 2+3 x 4=14 dimensions. L’ACM, à peu de choses près, consiste à projeter ce nuage sur ses « directions principales » qui sont déterminées comme dans une ACP. L’ACM est donc une forme d’ACP.
Quelques remarques doivent cependant être faites. D’abord, les variables indicatrices ne pouvant prendre que deux valeurs, les positions possibles sur chaque axe initial se réduisent à deux. Par ailleurs, les positions d’un individu sur les axes associés aux modalités d’une même variable ne peuvent pas être considérées comme indépendantes, la manière dont on construit presque toujours les variables qualitatives conduisant à ce qu’un individu se rattache à une et à une seule modalité. En conséquence, si les modalités des variables qualitatives jouent dans une ACM un rôle comparable aux variables quantitatives dans une ACP, le nuage des individus, bien que théoriquement représentable dans un espace qui compte autant de dimensions que de modalités, est en réalité un nuage de plus petite dimension, et le nombre de valeurs propres (« non nulles ») est inférieur au nombre de modalités (il est égal au nombre total de modalités auquel on soustrait le nombre de variables).
Une dernière particularité importante de l’ACP que constitue l’ACM est d’être pondérée : chaque variable indicatrice est dotée d’un poids d’autant plus élevé qu’elle est plus rare. Dans le repère initial, le nuage est donc plus étiré dans les directions associées aux modalités les plus rares, ce qui pèse dans la détermination des directions principales. Il faut en retenir que si l’ACM met en lumière un système de différences, elle rend particulièrement visibles les différences liées aux modalités les plus rares et les plus distinctives. Cet effet important ne s’observe cependant pas vraiment dans l’exemple des ministres, où les modalités ont été construites pour être à peu près équilibrées et correspondre, chacune, à une proportion grossièrement équivalente de la population étudiée (autour d’un tiers pour chacune des variables à trois modalités).
L’ACM détermine ici 14-5=9 axes. Les logiciels statistiques fournissent des résultats sur les valeurs propres (tableau 4).
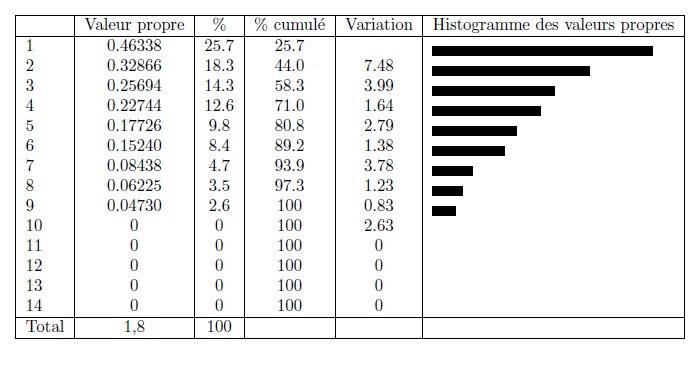
Tableau 4.
Les deux premiers axes correspondent à 25,7+18,3=44 % de la variance du nuage. La variance se dispersant nécessairement sur un assez grand nombre d’axes, on calcule parfois des « taux modifiés » qui atteindraient ici, pour les deux premiers axes, 96 %, indice qui peut pousser à n’étudier le nuage qu’au travers de ses projections sur les deux premiers axes. Les graphiques 8 et 9 donnent la représentation du nuage des modalités et des individus dans le premier plan factoriel.
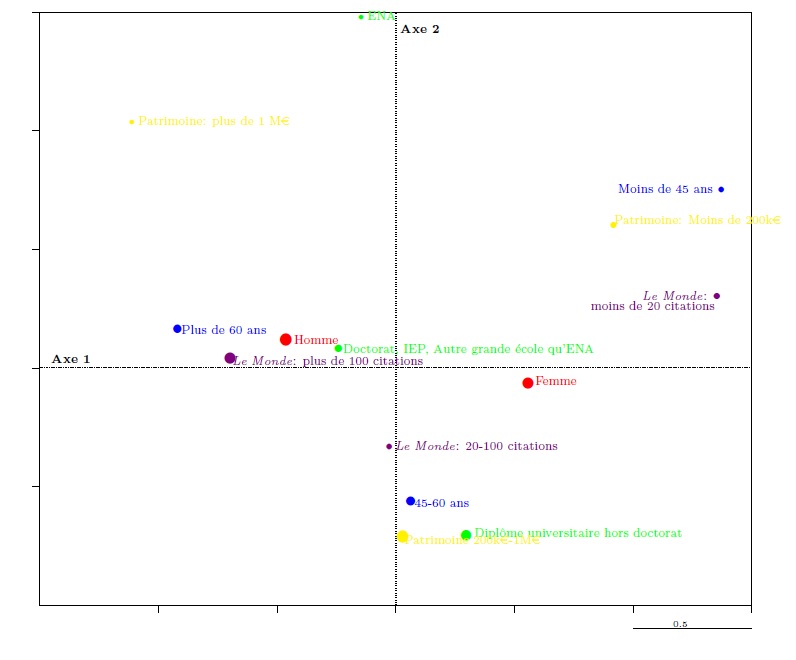
Graphique 8. Les caractéristiques des ministres dans le premier plan factoriel
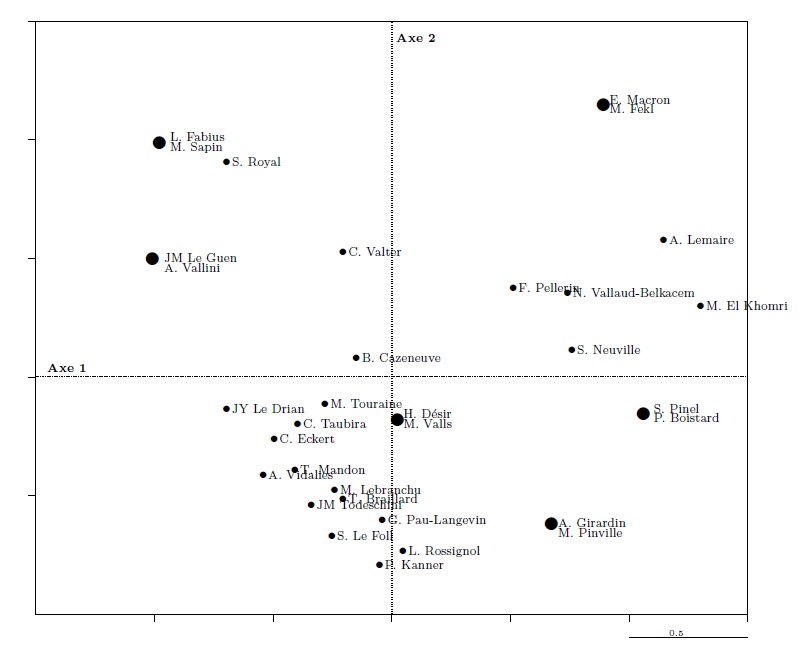
Graphique 9 : Les ministres dans le premier plan factoriel
Sur le graphique 8, le premier axe (l’axe horizontal) oppose (si l’on s’en remet à une « aide à l’interprétation » calculée par les logiciels et appelée « contribution [de la modalité] à l’axe » ; voir tableau 5), à droite de l’axe, la tranche d’âge, la tranche de patrimoine et les nombres de citations dans Le Monde les moins élevés et, à gauche de l’axe, la tranche d’âge, la tranche de patrimoine et les nombres de citations dans Le Monde les plus élevés. Ce premier axe oppose à gauche, M. El Khomri, A. Lemaire, S. Pinel, P. Boistard, E. Macron et quelques autres ministres (également jeunes) et de l’autre A. Vallini, J.-M. Le Guen, M. Sapin, L. Fabius, S. Royal, J.-Y. Le Drian. Le principe de différences le plus puissant (au regard des variables retenues dans l’analyse) a donc manifestement à voir avec l’âge et des caractéristiques qui tendent à lui être liées, au moins parmi les ministres étudiés, comme le patrimoine personnel ou la notoriété des ministres.
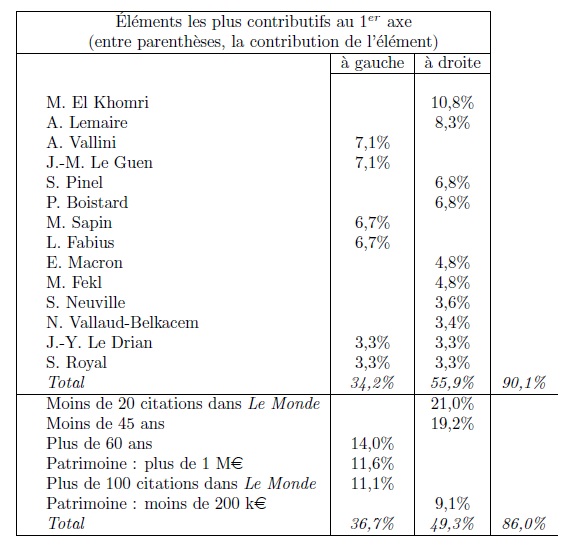
Tableau 5. L'interprétation de l’axe 1
Le deuxième axe renvoie à une différence moins puissante, mais néanmoins lisible. Il oppose, en haut (voir Tableau 6) du graphique 8, les tranches d’âge et de patrimoine extrêmes mais surtout le passage par l’ENA et, en bas du graphique 8, les diplômes proprement universitaires (doctorat mis à part) et les tranches d’âge et de patrimoine moyennes. Parmi les ministres, il oppose des diplômés de l’ENA d’âges différents (E. Macron, M. Fekl, M. Sapin, L. Fabius, S. Royal) et des ministres appartenant à la tranche d’âge moyenne et qui ne sont pas passés par une grande école (ni par un IEP ou un doctorat). L’analyse ne peut être poussée très loin, compte tenu du faible nombre de variables intégrées à l’analyse, mais l’on peut penser que l’axe renvoie à une différence qui tient à la formation scolaire (et notamment le passage par l’ENA) et à ses effets sur les trajectoires politiques.
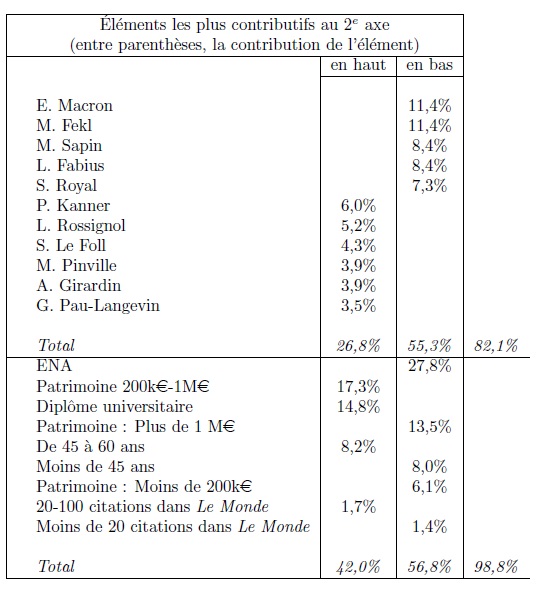
Tableau 6. L'interprétation de l’axe 2
L’exemple permet de formuler quelques propriétés des graphiques d’ACM utiles pour leur lecture.

Jozef Krakovsky, 82-11 (2011)
Les deux types de graphiques que produit « en sortie » une ACM sont solidaires. Par exemple, sur le graphique des individus, les ministres les plus âgés se trouvent du même côté de l’axe 1 que la tranche d’âge la plus élevée sur le graphique des modalités. Les graphiques conduisent en effet à explorer un tableau (tableau 3) qui peut être lu en ligne (les individus) ou en colonne (les variables et leurs modalités).
Les graphiques des individus et les graphiques des modalités dans une ACM sont unis par une relation barycentrique : sur le graphique des individus, on peut par exemple distinguer les ministres en fonction de leur tranche d’âge, en usant de couleurs différentes (graphique 10) ; si l’on construit pour chaque tranche d’âge le barycentre des points associés aux ministres concernés, les trois points associés aux trois tranches d’âge se répartissent dans l’espace de la même manière que les points représentant les tranches d’âge sur le graphique 8 (ils sont simplement un peu plus proches de l’origine).
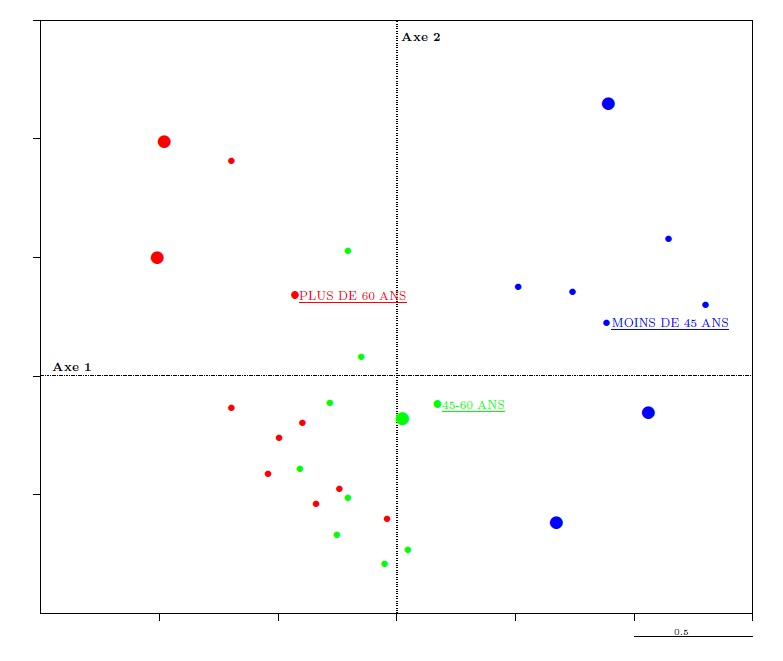
Graphique 10. La construction de points-modalités dans le nuage des individus
Cette observation se vérifie dans l’autre sens : on peut, sur le graphique des modalités, construire le barycentre des modalités auxquels se rattache l’un des ministres (par exemple Ségolène Royal sur le graphique 11) ; ce barycentre se situe dans le même cadran que le point représentant le ministre concerné sur le graphique 9.
Jozef Krakovsky, Ma rouge (2007)
On comprend du même coup que, si sur le graphique 9, S. Royal se trouve représentée par un point très proche, mais légèrement plus bas et plus à droite, que L. Fabius et M. Sapin, c’est qu’elle ne diffère d’eux que par une variable qui la déporte légèrement vers le Sud-Est (le point « femme » n’est que légèrement éloigné du point « hommes », mais l’est dans une direction Sud-Est).
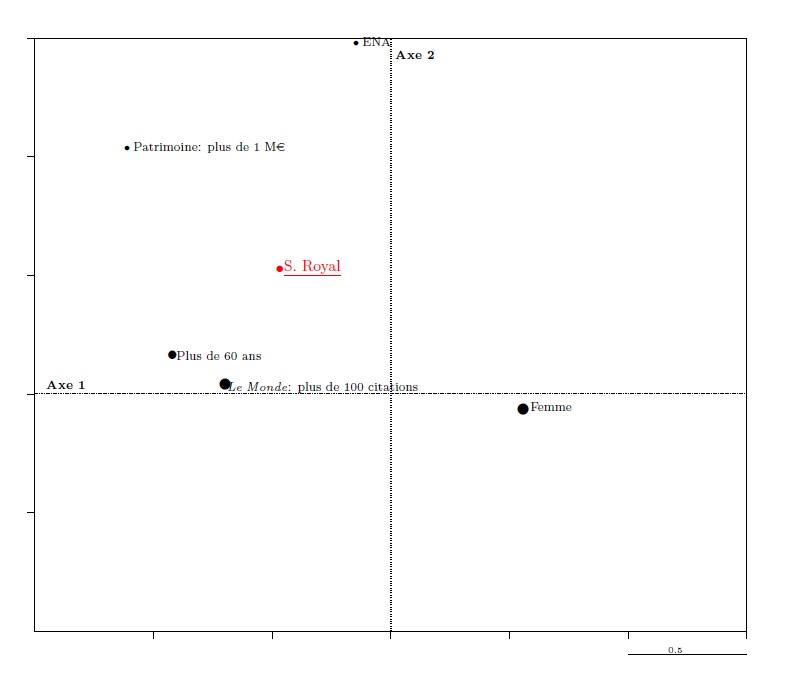
Graphique 11. La construction d’un point-individu dans le nuage des modalités
Au passage, on peut observer que les « individus statistiques » se réduisent à leur profil statistique : L. Fabius et M. Sapin sont représentés par un même point sur le graphique 9 parce qu’ils sont interchangeables au regard des variables retenues dans l’analyse (mais ils constituent deux individus « réels » évidemment distincts et pourraient être représentés par des points très différents si d’autres variables avaient été utilisées dans l’ACM).
La proximité de deux modalités sur les premiers axes factoriels indique qu’elles ont une certaine probabilité d’être réunies par les mêmes individus mais cette probabilité ne peut être estimée que par un retour au tableau 3 : ainsi, « moins de 45 ans » et « patrimoine inférieur à 200 000 € » sont proches sur le graphique 8, mais 3 des 8 ministres de moins de 45 ans ont déclaré un patrimoine supérieur.
Dans une ACM, les modalités d’une même variable forment un sous-nuage de points qui se répartissent toujours de part et d’autre du centre du graphique : sur le graphique 8 où les variables sont repérées par des couleurs différentes, les points d’une même couleur peuvent être assez proches (pour le sexe en rouge) ou éloignés les uns des autres (pour la formation en vert) mais ils se répartissent toujours entre des cadrans opposés. Il s’agit là encore d’une propriété barycentrique : le centre des axes est le barycentre pondéré des points associés aux modalités d’une même variable. Il en résulte, pour les variables à deux modalités, que celles-ci se trouvent sur une même droite qui passent par le centre et que leurs distances au centre des axes ramène à leurs fréquences dans la population : pour le sexe (graphique 11), le rapport dfdh est égal au rapport entre le nombre d’hommes et de femmes : 17/16=1,0625. C’est le principe dit du « bras de levier ».
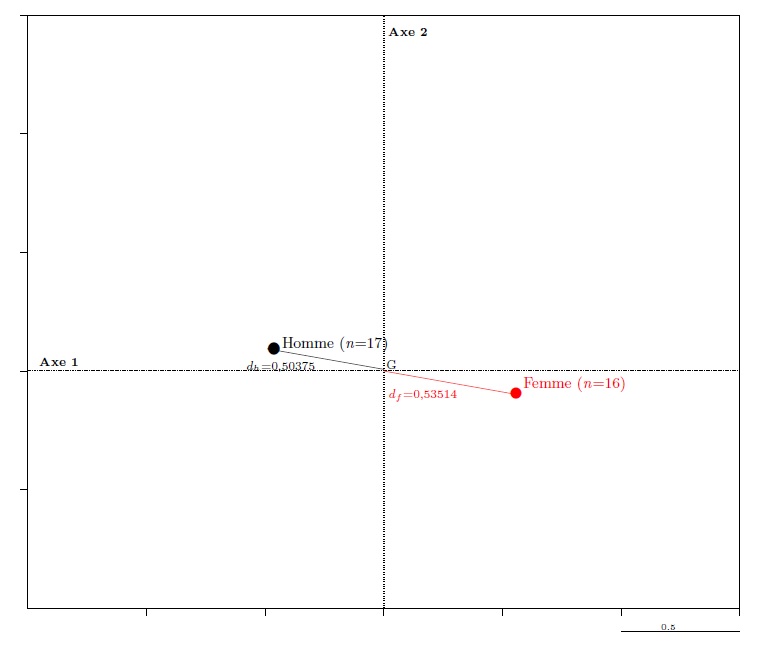
Graphique 12. Le « principe du bras de levier »
Deux modalités d’une variable dichotomique s’opposent donc mécaniquement sur tous les axes d’une ACM. Par conséquent, il n’est possible de conclure à une opposition structurante au sein de la population étudiée que dans le cas où elles sont excentrées par rapport à l’origine des axes. Ici, les positions des modalités « hommes » et « femmes » sur les deux premiers axes indiquent que les hommes sont légèrement sur-représentés parmi les ministres énarques, les ministres âgés ou les ministres dotés de gros patrimoines et que les femmes sont à l’inverse un peu plus nombreuses parmi les plus jeunes, les moins cités dans Le Monde avant l’élection de François Hollande, etc. Les deux modalités, cependant, restent assez proches du centre des axes : le sexe ne peut pas être considéré ici comme un principe de différenciation très puissant, et le graphique 13 montre que si chaque cadran du graphique se caractérise par une surreprésentation masculine ou féminine assez nette, tous sont « mixtes » (on peut comparer avec le graphique 10, où les ministres les plus jeunes et les plus âgés sont totalement absents de certains cadrans). Cela peut tenir, au moins en partie, à ce que dans une ACM les variables qui apparaissent comme les plus « structurantes » sont souvent celles qui ont le plus de modalités.
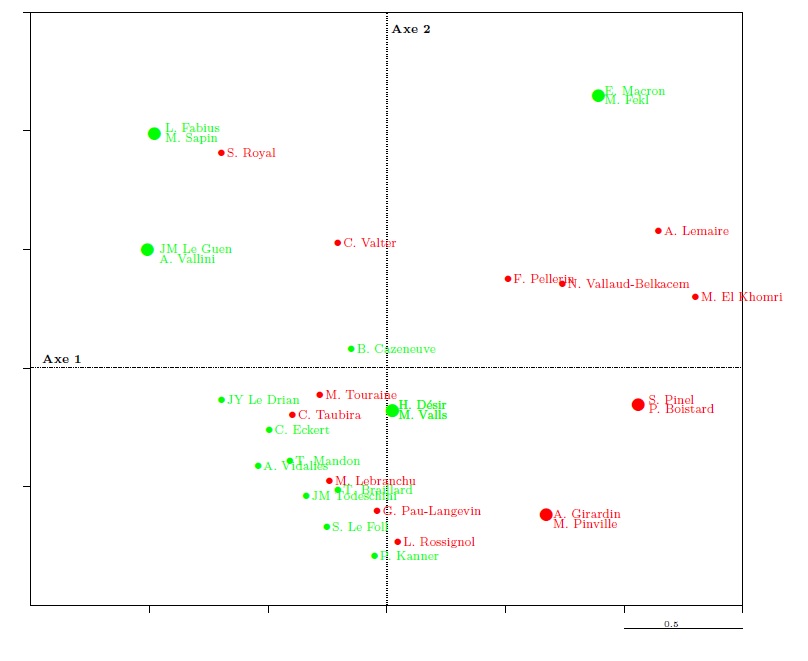
Graphique 13. Le nuage des ministres, marqués selon le sexe
Une fois les plans factoriels interprétés, on y projette parfois des éléments qualifiés d’« illustratifs » ou de « supplémentaires » pour ne pas être confondus avec les éléments « actifs » qui contribuent à la construction des axes. Cette pratique repose sur les propriétés barycentriques déjà évoquées.
On peut par exemple projeter dans le nuage des modalités la variable supplémentaire qui distingue les ministres et les secrétaires d’État. Les deux modalités (voir graphique 14) se projettent près du centre, ce qui indique que le fait d’être ministre ou secrétaire d’État n’est que faiblement lié aux deux grands principes de structuration des données, même si la probabilité d’être ministre paraît (légèrement) plus grande chez les détenteurs des propriétés dominantes (passage par l’ENA, âge élevé, hommes, etc.).
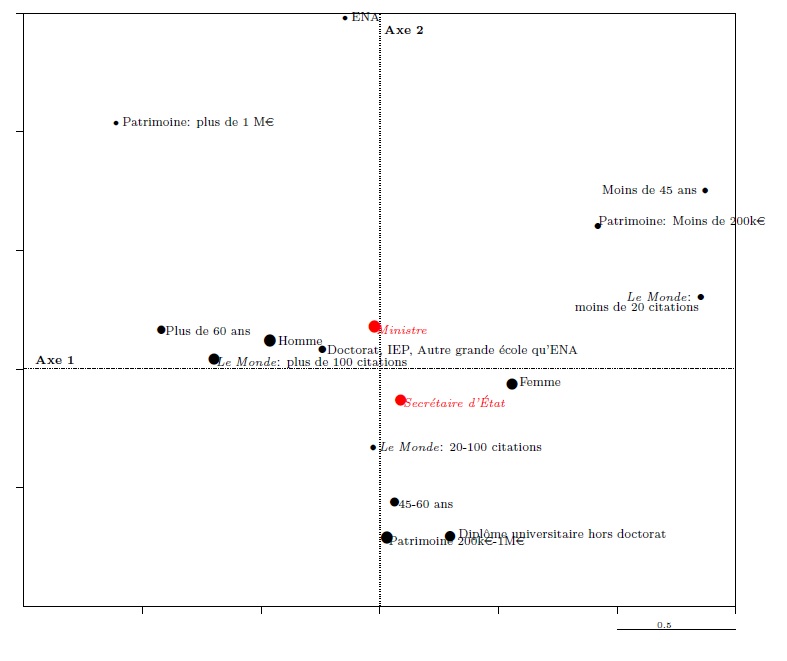
Graphique 14. La projection d’une variable supplémentaire
De manière analogue, il est possible de projeter dans le nuage des individus des personnes supplémentaires, par exemple le président de la République, François Hollande. Celui-ci, se projette sur le même point que Laurent Fabius ou Michel Sapin, dont il est proche par le profil.
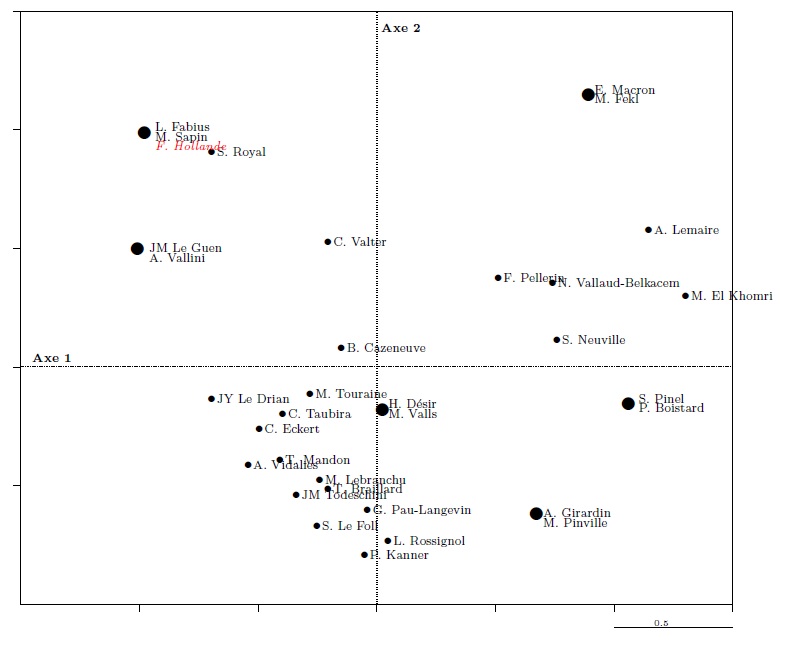
Graphique 15. La projection d’un individu supplémentaire
En prolongement de l’ACM, d’autres méthodes statistiques peuvent être utilisées. La plus couramment mise en œuvre est la classification qui peut aider à utiliser les résultats de l’ACM pour construire des classes ou des typologies, en distinguant plusieurs types de ministres (graphique 16).
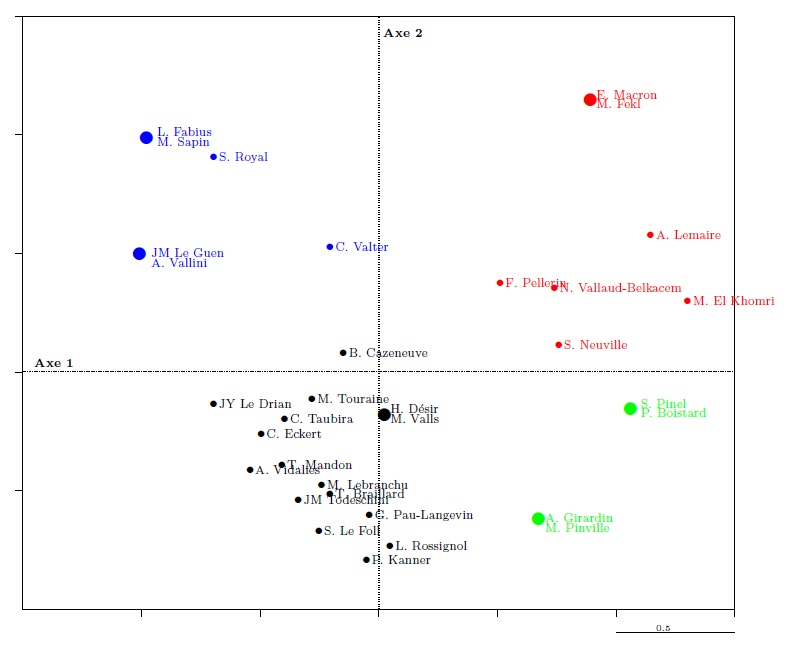
Graphique 16. La classification ascendante hiérarchique des ministres
L’ACM et la construction des champs
Un mot peut être dit pour finir de l’usage spécifique que Pierre Bourdieu a fait de l’ACM. L’intérêt que le sociologue a exprimé, à plusieurs reprises, pour cette méthode statistique25 traduit sans doute, comme le note Alain Desrosières, une parenté de son entreprise avec celle de Jean-Paul Benzecri : les deux hommes furent, chacun dans leur discipline respective, innovateurs et critiques d’une forme d’impérialisme théorique ou méthodologique états-unien26. Ils s’étaient côtoyés à l’École normale supérieure et ont eu des échanges en quelques occasions, notamment lors d’une journée d’études à la Sorbonne en 197827. Pour autant, Bourdieu ne partageait assurément pas la totalité des vues de Benzecri parfois très imprégnées de thomisme28 et de substantialisme29. S’il pouvait se reconnaître dans certaines orientations de « l’école française d’analyse des données », il s’est réellement approprié l’outil, l’intégrant à sa sociologie et à la réflexion sur la pratique statistique qu’il avait ouverte dès ses enquêtes en Algérie avec des administrateurs de l’INSEE.

Jozef Krakovsky, Du cycle Lignes N° 3 (2011)
Il a découvert l’ACM au moment où « l’analyse des données » émergeait, et ne s’en est pas détourné par la suite. Il la mobilise dans un article de 1976 sur l’« anatomie du goût »30, puis de nouveau en 1978 dans une étude du patronat31 et, au cours des années 1980, dans ses livres sur le champ universitaire32, les grandes écoles33, dans son enquête sur la politique du logement34 et, sensiblement plus tard, dans l’une de ses dernières recherches qui porte sur l’édition35. Le travail sur l’épiscopat a aussi supposé la réalisation d’une ACM même si elle n’a pas été publiée36. Quant au schéma souvent reproduit qui distribue les attributs du style de vie et les groupes sociaux dans un diagramme en deux dimensions, il ne résulte pas directement d’une ACM, mais il en est marqué par l’esprit37.
Le recours à l’ACM chez Bourdieu n’est pas séparable de l’usage de la notion de champ. Un enjeu des ACM dans La Distinction est l’élaboration de ce qu’il appelle « l’espace social » ou, quelquefois, « champ social » ou « champ des classes sociales ». Les ACM sur le patronat, les universitaires, les hauts-fonctionnaires, l’épiscopat, les grandes écoles participent de la série de travaux qu’il engage à la fin des années 1970 sur les différentes régions de ce qu’il appelle de plus en plus souvent, au cours de la décennie suivante, le « champ du pouvoir ». Toutes les publications de Bourdieu consacrées à des champs particuliers ne comportent pas d’ACM ; certaines d’entre elles, qui entreprennent d’élargir l’application du concept de champ (au droit, au journalisme, à la science38), n’ont en effet pas donné lieu à des enquêtes prosopographiques approfondies. Engagé avant l’émergence de « l’analyse des données », et de caractère historique, le travail sur le champ littéraire39 n’en comporte pas non plus mais certains de ses passages et schémas pourraient être comparés à de quasi-ACM ou à des ACM « imaginaires »40, comme le montre un schéma de la structure des champs de production culturelle ou un autre qui emboîte champ intellectuel, champ du pouvoir et espace social.
Bourdieu se tourne vers l’ACM lorsque les méthodes d’« analyse de données » se diffusent, mais aussi au début de la période où le concept de « champ » devient central dans sa théorie sociale. C’est autour de 1970 qu’il se met à faire un usage intensif de la notion, notamment à la suite de ses relectures de la sociologie religieuse de Max Weber41. On peut d’ailleurs relever que ces relectures comportent un schéma qui, sous la forme d’un ensemble de flèches, vise à restituer le système de relations qui s’établit entre les prêtres, les prophètes, les sorciers et les laïcs. C’est un autre type de représentation des « champs » qu’il propose, quelques années plus tard, en s’aidant de l’ACM. John Levi Martin souligne que si Bourdieu n’est pas le seul auteur d’une « théorie des champs » en sciences sociales à avoir recherché un outil de visualisation, il a trouvé avec l’ACM un instrument particulièrement adapté42.
C’est que l’ACM conduit, on l’a vu, à travailler sur des systèmes de différences. Elle se concentre sur des écarts à la moyenne. Elle donne une importance particulière aux modalités rares, c’est-à-dire aux caractéristiques les plus distinctives. Elle se prête par là au raisonnement relationnel que prône Bourdieu, notamment au travers du concept de champ. Rendant visible une structure à partir d’informations qui sont la plupart du temps collectées au niveau des individus, elle aide à se départir des conceptions du monde social qui font de l’individu la réalité ultime pour s’attacher à ces « systèmes de relations » dont Bourdieu peut dire qu’ils sont le « véritable sujet » des actions sociales ou que leur construction constitue « l’objectif majeur de la science sociale »43. Bourdieu, par comparaison avec d’autres utilisateurs de l’ACM, prête beaucoup d’attention aux « nuages des individus » dans les plans factoriels ; ces graphiques aident à appréhender les individus pour ce qu’ils sont à ses yeux : non pas des « substances » interchangeables mais des agents socialisés situés les uns par rapport aux autres, occupants de positions (et porteurs de propriétés) spécifiques.
L’ACM aide ainsi à objectiver des espaces théoriques dont Bourdieu parle comme d’une « réalité invisible, que l’on ne peut ni montrer ni toucher du doigt, et qui organise les pratiques et les représentations des agents »44. L’usage qu’il en a fait répond en un sens à cet espoir de Benzecri que l’analyse factorielle révèle des « réalités » qui, comme en d’autres temps des grandeurs physiques telles que l’énergie ou la charge électrique, doivent être « conjecturées » avant d’être « reconnues pour exister »45. La capacité de l’ACM à extraire des « facteurs principaux » d’une « mer de données » répond au souci des analyses en termes de champ de dégager des principes de différenciation fondamentaux, là où l’observation de la vie sociale peut faire apparaître, mais sans parvenir à les hiérarchiser, des principes de différences en nombre quasiment illimité. L’ACM contribue de fait dans La Distinction à consacrer le volume et la structure du capital comme principes fondamentaux des goûts culturels, dotés d’un pouvoir explicatif plus grand là où tant de déterminants qui peuvent leur être liés sont ordinairement convoqués (l’âge, le lieu de résidence, le sexe, l’appartenance « ethnique », etc.) Mais si Bourdieu exploite la capacité de l’ACM à extraire des « facteurs principaux » permettant de visualiser la « structure des champs », c’est de l’ensemble des résultats des ACM qu’il entreprend de tirer profit. La distribution des individus statistiques et des modalités dans les plans factoriels est, dans ses travaux, examinée de façon approfondie. Elle aide à comprendre les « pôles » en présence, les rapports de forces entre les porteurs de différentes espèces de capitaux.
Jozef Krakovsky, Du cycle Lignes N° 7 (2011)
Ainsi, Bourdieu a non seulement exploité de façon précoce les propriétés géométriques de l’ACM46, mais il a aussi tiré profit de ses affinités avec un raisonnement relationnel et en a fait un outil d’objectivation de ces « espaces théoriques » que sont les champs. Outil de construction et d’objectivation, l’ACM a aussi nourri ses réflexions sur les implications des opérations d’objectivation : le seul texte à caractère méthodologique qu’il lui a consacré47 souligne la valeur de la méthode, en même temps qu’il met en garde contre le risque d’« objectivisme » qu’elle renferme. La pratique de l’ACM a également sans doute beaucoup nourri le chapitre d’ouverture d’Homo Academicus48 qui s’interroge sur ce qu’impliquent les opérations d’objectivation par lesquelles la sociologie met en évidence la structure d’un espace ou la distribution de capitaux qui ne sont que partiellement objectivés dans la réalité sociale. L’usage très remarqué de l’ACM par Bourdieu représente un cas somme toute assez rare d’articulation très étroite entre une théorie sociale et une méthode statistique.
Avec le concept de champ, c’est indissociablement la notion de capital qui est engagée dans les usages de l’ACM par Bourdieu. Les tableaux qu’il soumet à l’ACM consistent presque toujours en des matrices renseignant, pour une population d’agents sociaux ou d’institutions efficientes dans l’espace social analysé, des indicateurs relatifs aux formes de capital efficientes dans celui-ci. Leur élaboration suppose une interrogation sur le capital ; comme l’écrit Bourdieu, « pour construire l’espace social, dans le cas de la France, il fallait et il suffisait de prendre en compte les différentes espèces de capital dont la distribution détermine la structure de l’espace social »49. Sachant que l’ACM ne permet jamais que de regarder, sous un angle différent, l’information que l’on fait figurer dans le tableau « en entrée », Bourdieu, dans sa façon de procéder, illustre très bien l’observation de Benzecri selon laquelle si « une analyse de données n’est, en bonne mathématique, qu’une recherche de vecteurs propres, toute la science, ou tout l’art [est] de savoir quelle matrice traite ! »50. Quand Bourdieu recourt à l’ACM, la construction de la « matrice » donne lieu à des considérations très substantielles sur la question des limites, des frontières des champs ou sur l’efficience des différentes espèces de capitaux ; elle affronte cette sorte de « cercle herméneutique » qui, bien qu’inhérent au travail de statistique, est très souvent refoulé dans les travaux « quantitatifs » en sciences sociales51.
L’interrogation autour de la notion de capital se poursuit devant les résultats des ACM, le premier axe renvoyant presque toujours au volume de capital, le second à sa structure, les suivants à des principes plus secondaires (le mode d’acquisition du capital par exemple dans La Distinction). L’ACM, utilisée par Bourdieu, aide à construire à la fois la structure du champ et la distribution du capital. Elle est un instrument de synthèse qui fait surgir d’informations imparfaites, ambiguës (les variables actives sont en effet toujours d’une série d’indicateurs disparates, constitués sous des contraintes fortes du fait que les différentes formes de capital sont inégalement objectivées dans la réalité et inégalement objectivables), des indicateurs plus abstraits et plus pertinents. Seul un outil comme l’ACM peut mettre en évidence empiriquement ces formes fondamentales de capital (« capital économique », « capital culturel », capital spécifique à un champ, etc.) dont il n’existe aucun indicateur simple. C’est par l’agrégation ou la synthèse des variables actives à laquelle procède l’ACM que ces capitaux se manifestent.
La même remarque vaudrait s’agissant du « volume de capital », expression directement issue de la pratique de l’ACM. Bourdieu sait que cette notion confine, à certains égards, à l’artefact statistique. Elle est en effet très abstraite et difficile à définir autrement que comme une variante de « l’effet de taille » bien connu des praticiens de l’analyse factorielles : le « volume de capital » est ce principe de structuration fondamental qui émerge d’une ACM quand les variables actives consistent en des indicateurs de capitaux diversifiés. Mais cette notion, née de l’agrégation un peu obscure qui se réalise dans la « boîte noire » de l’ACM, soulève simultanément des questions très importantes. Elle vient fonder empiriquement cette opposition fondamentale, commune, semble-t-il, à tous les univers sociaux, entre « dominants » et « dominés » ; elle conduit à réfléchir au problème de la convertibilité des différentes espèces de capitaux et à celui de l’unité que conserve le « capital », au-delà des différentes formes sous lesquelles il se spécifie.
Notes
1
Pierre Bourdieu, La Distinction. Critique sociale du jugement, Paris, Éditions de Minuit, 1979, p. 189.
2
Brigitte Le Roux, Analyse géométrique des données multidimensionnelles, Paris, Dunod, 2014.
3
Jean-Paul Benzecri, L’Analyse des données. 2 : L’analyse des correspondances, Paris, Bordas, 1973, p. 8.
4
Pour un exemple à ce sujet, voir ce que Jean-Paul Benzecri dit de l’étude, liée à une problématique de l’époque, de la relation entre la lecture et la possession d’un poste de télévision (L’Analyse des données. 2 : L’analyse des correspondances, Paris, Bordas, 1973, p. 10-12).
5
Jean-Paul Benzecri, L’Analyse des données. 2 : L’analyse des correspondances, Paris, Bordas, 1973, p. 3.
6
Idem, p. 6.
7
Jean-Paul Benzecri, L’Analyse des données. 1 : La taxinomie, Paris, Bordas, 1973, p. 590
8
Jean-Paul Benzecri, L’Analyse des données. 2 : L’analyse des correspondances, Paris, Bordas, 1973, p. 10.
9
Idem, p. 16.
10
Jean-Paul Benzecri, L’Analyse des données. 1 : La taxinomie, Paris, Bordas, 1973, p 590.
11
Sur l’histoire de cette école et sur la diffusion de ces méthodes dans les années 1970, voir : Michel Armatte, « Histoire et Préhistoire de l'Analyse des données par J.-P. Benzecri : un cas de généalogie rétrospective », Electronic Journ@l for History of Probability and Statistics, vol. 4, n° 2, 2008 ; Philippe Bonnet, « Pour une histoire sociale de l’analyse des données », in F. Lebaron, B. Le Roux (dir.), La Méthodologie de Pierre Bourdieu en action. Espace culturel, espace social et analyse des données, Paris, Dunod, 2015, p. 21-42.
12
Alain Desrosières, « Analyse des données et sciences humaines : comment cartographier le monde social ? », Electronic Journ@l for History of Probability and Statistics, vol. 4, n° 2, 2008.
13
Michel Volle, Analyse des données, Paris, Economica, 1978 (4e édition en 1997).
14
Ludovic Lebart, Marie Piron, Alain Morineau, Statistique exploratoire multidimensionnelle. Visualisation et inférence en fouille de données, Paris, Dunod, 2006 [4e édition].
15
Yvonne Bernard, « Faits sociaux et jugements de goût », Revue française de sociologie, vol. 11, n° 2, 1970, p. 179-196.
16
Lucie Tanguy, « L'État et l'école. L'école privée en France », Revue française de sociologie, vol. 13, n° 3, 1972, p. 325-375 ; Michèle Salitot-Dion, « Rôle du mariage dans l'accumulation des patrimoines chez les agriculteurs », Revue française de sociologie, vol. 16, n° 1, 1975, p. 59-78.
17
Sur la diffusion internationale de l’analyse des correspondances, voir Philippe Bonnet, « Pour une histoire sociale de l’analyse des données », in F. Lebaron, B. Le Roux (dir.), La Méthodologie de Pierre Bourdieu en action. Espace culturel, espace social et analyse des données, Paris, Dunod, 2015, p. 21-42 ; Brigitte Le Roux, Henry Rouanet, Geometric Data Analysis, Dordrecht, Kluwer, 2004, p. 11-13.
18
Ece Kumbasar, Rommey A. Kimball, William H. Batchelder, « Systematic Biases in Social Perception », American Journal of Sociology, vol. 100, n° 2, 1994, p. 477-505 ; David R. Gibson, « Taking Turns and Talking Ties : Networks and Conversational Interaction », American Journal of Sociology, vol. 110, n° 6, 2005, p. 1561-1597.
19
Brigitte Le Roux, Henry Rouanet, Multiple Correspondence Analysis, Thousand Oaks, Sage, 2010.
20
Pour quelques références, voir : Tony Bennett, Mike Savage, Elizabeth Silva, Alan Warde, Modesto Gayo-Cal, David Wright, Culture, Class Distinction, Londres, Routledge, 2009 ; Johannes Hjellbrekke, Olav Korsnes, « Quantifying the Field of Power in Norway », in K. Robson, C. Sanders (dir.) Quantifying Theory : Pierre Bourdieu, Toronto, Springer Netherlands, 2009, p. 31–46 ; Virgilio Borges Pereira, Classes e Culturas de Classe das Famílias Portuenses. Classes sociais e «modalidades de estilização da vida» na cidade do Porto, Porto, Afrontamento/Instituto de Sociologia da Faculdade de Letras da Universidade do Porto, 2005 ; Annick Prieur, Lennart Rosenlund, Jacob Skjott-Larsen, « Cultural capital today : a case study from Denmark », Poetics, vol. 36, n° 1, 2008, p. 45-71 ; Lennart Roselund, « Cultural change in Norway : cultural and economic dimensions », International Journal of Contemporary Sociology, vol. 37, n° 2, 2000, p. 245-275.
21
Pour une revue assez détaillée des usages de l’ACM en sociologie de la culture, voir Julien Duval : « Multiple Correspondence Analysis », in D. Inglis, A.-M. Almila (dir.), The SAGE Handbook of Cultural Sociology, London, SAGE, 2016, p. 255-271.
22
Les termes sont de Jean-Pierre Courtial : « À propos de l'analyse des données. Pour un dialogue entre méthodologue et chercheur », Revue française de sociologie, vol. 19, n° 4, 1978, p. 585.
23
Voir sur ce point : Brigitte Le Roux, Henry Rouanet, Geometric Data Analysis, Dordrecht, Kluwer, 2004 ; Brigitte Le Roux, Henry Rouanet, Multiple Correspondence Analysis, Thousand Oaks, Sage, 2010 ; Brigitte Le Roux, Analyse géométrique des données multidimensionnelles, Paris, Dunod, 2014.
24
Voir le Site Internet ci-dessous.
25
Voir, par exemple, « Je suis un peu comme un vieux médecin qui connaît toutes les maladies de l’entendement sociologique. Entretien recueilli par Beate Krais », in P. Bourdieu, J.-C. Chamboredon, J.-C. Passeron, Le Métier de sociologue [1967], Berlin-New York, Mouton de Gruyter, 2005 [5e édition], p. xiii-xiv.
26
Alain Desrosières, « Analyse des données et sciences humaines : comment cartographier le monde social ? », Electronic Journ@l for History of Probability and Statistics, vol. 4, n° 2, 2008.
27
Voir notamment : Jean-Paul Benzecri, « In memoriam : Pierre Bourdieu », Modulad, n° 35, 2006.
28
Karl Van Meter, Marie-Ange Schiltz, Philippe Cibois, Lise Mounier, « History and French Sociological Perspective », in M. Greenacre, J. Blasius (dir.), Correspondence Analysis in the Social Sciences, Londres, Academic Press, 1994, p. 128-137.
29
Le texte assez tardif de Jean-Paul Benzecri sur Cassirer (« Substance et fonction, éléments pour une théorie du concept », Les Cahiers de l’analyse des données, vol. 3, n° 2, 1978, p. 239-242), n’est sans doute pas étranger à l’influence, directe ou indirecte, exercée par Bourdieu.
30
Pierre Bourdieu, Monique de Saint Martin, « Anatomie du goût », Actes de la recherche en sciences sociales, n° 5, 1976, p. 3-81. Cet article (et ses ACM) sont repris sous une forme remaniée dans différents chapitres de La Distinction (Paris, Éditions de Minuit, 1979).
31
Pierre Bourdieu, Monique de Saint Martin, « Le patronat », Actes de la recherche en sciences sociales, n° 20/21, 1978, p. 3-82.
32
Pierre Bourdieu, Homo Academicus, Paris, Éditions de Minuit, 1984.
33
Pierre Bourdieu, La Noblesse d’État. Grandes écoles et esprit de corps, Paris, Éditions de Minuit, 1989.
34
Pierre Bourdieu, Rosine Christin, « La construction du marché. Le champ administratif et la production de la “politique du logement” », Actes de la recherche en sciences sociales, n° 81/82, 1990, p. 65-85 (cet article est repris dans : P. Bourdieu, Les Structures sociales de l’économie, Paris, Le Seuil, 2000).
35
Pierre Bourdieu, « Une révolution conservatrice dans l’édition », Actes de la recherche en sciences sociales, n° 126-127, 1999, p. 3-28, 1999.
36
Pierre Bourdieu, Monique de Saint Martin, « La sainte famille. L'épiscopat français dans le champ du pouvoir », Actes de la recherche en sciences sociales, n° 44-45, 1982, p. 2-53.
37
Ce graphique, déjà présent dans « Anatomie du goût » (Actes de la recherche en sciences sociales, n° 5, 1976, p. 3-81), est repris dans La Distinction (Paris, Éditions de Minuit, 1979), assorti d’une note sur sa construction (voir p. 139), et sous une forme simplifiée dans Raisons pratiques. Sur la théorie de l’action (Paris, Le Seuil, 1994, p. 21).
38
Pierre Bourdieu, « Le champ scientifique », Actes de la recherche en sciences sociales, n° 2/3, 1976, p. 88-104 ; « La force du droit. Éléments pour une sociologie du champ juridique », Actes de la recherche en sciences sociales, n° 64, 1986, p. 5-19 ; Sur la télévision suivi de « L’emprise du journalisme », Paris, Raisons d’agir, 1996.
39
Pierre Bourdieu, Les Règles de l’art. Genèse et structure du champ littéraire, Paris, Le Seuil, 1992.
40
Le terme s’entend au sens où l’on parle d’« expériences imaginaires ». Reprenant, pour une période ultérieure, les analyses de Bourdieu sur le champ littéraire, Gisèle Sapiro proposera des ACM bien réelles. Voir par exemple : G. Sapiro, « La raison littéraire. Le champ littéraire français sous l'Occupation (1940-1944) », Actes de la recherche en sciences sociales, n° 111, 1996, p. 3-35 ; G. Sapiro, La Guerre des écrivains, Paris, Fayard, 1999.
41
Voir : Pierre Bourdieu, « Genèse et structure du champ religieux », Revue française de sociologie, vol. 12, n° 3, 1971, p. 295-334 ; « Une interprétation de la théorie de la religion selon Max Weber », Archives européennes de sociologie, vol. 12, n° 1, 1971, p. 3-21.
42
John Levi Martin, « What is field theory? », American Journal of Sociology, vol. 109, n° 1, 2003, p. 1-49.
43
Pierre Bourdieu, Raisons pratiques. Sur la théorie de l’action, Paris, Le Seuil, 1994, p. 54-55.
44
Pierre Bourdieu, Raisons pratiques. Sur la théorie de l’action, Paris, Le Seuil, 1994, p. 25.
45
Jean-Paul Benzecri, L’Analyse des données. 2 : L’analyse des correspondances, Paris, Bordas, 1973, p. 7.
46
Henry Rouanet, Werner Ackermann, Brigitte Le Roux, « The lesson of Bourdieu’s La Distinction », Bulletin de méthodologie sociologique, n° 65, 2000, p. 5-18.
47
Il s’agit du texte placé en avant-propos à l’article sur le patronat : Pierre Bourdieu, Monique de Saint Martin, « Le patronat », Actes de la recherche en sciences sociales, n° 20/21, 1978, p. 3-8.
48
Pierre Bourdieu, Homo Academicus, Paris, Éditions de Minuit, 1984, p. 9-52.
49
Pierre Bourdieu, Raisons pratiques. Sur la théorie de l’action, Paris, Le Seuil, 1994, p. 32.
50
Jean-Paul Benzecri, L’Analyse des données. 1 : La taxinomie, Paris, Bordas, 1973, p. 590.
51
Sur la manière dont Bourdieu construit ses tableaux, voir notamment : Julien Duval, « L'analyse des correspondances et la construction des champs », Actes de la recherche en sciences sociales, n° 200, 2013, p. 110-123.
Bibliographie
Michel Armatte, 2008, « Histoire et Préhistoire de l'Analyse des données par J.-P. Benzecri : un cas de généalogie rétrospective », Electronic Journ@l for History of Probability and Statistics, vol. 4, n° 2..
Jean-Paul Benzecri, L’Analyse des données. 1 : La taxinomie, Paris, Bordas, 1973.
Jean-Paul Benzecri, L’Analyse des données. 2 : L’analyse des correspondances, Paris, Bordas, 1973.
Jean-Paul Benzecri, « Substance et fonction, éléments pour une théorie du concept », Les Cahiers de l’analyse des données, vol. 3, n° 2, 1978, p. 239-242.
Jean-Paul Benzecri, « In memoriam : Pierre Bourdieu », Modulad, n° 35, 2006.
Philippe Bonnet, « Pour une histoire sociale de l’analyse des données », in Frédéric Lebaron, Brigitte Le Roux (dir.), La Méthodologie de Pierre Bourdieu en action. Espace culturel, espace social et analyse des données, Paris, Dunod, 2015, p. 21-42.
Tony Bennett, Mike Savage, Elizabeth Silva, Alan Warde, Modesto Gayo-Cal, David Wright, Culture, Class Distinction, Londres, Routledge, 2009.
Yvonne Bernard, « Faits sociaux et jugements de goût », Revue française de sociologie, vol. 11, n° 2, 1970, p. 179-196.
Pierre Bourdieu, « Genèse et structure du champ religieux », Revue française de sociologie, vol. 12, n° 3, 1971, p. 295‑334.
Pierre Bourdieu, « Une interprétation de la théorie de la religion selon Max Weber », Archives européennes de sociologie, vol. 12, n° 1, 1971, p. 3‑21.
Pierre Bourdieu, « Le champ scientifique », Actes de la recherche en sciences sociales, n° 2/3, 1976, p. 88-104, 1976.
Pierre Bourdieu, La Distinction. Critique sociale du jugement, Paris, Minuit, 1979.
Pierre Bourdieu, Homo Academicus, Paris, Minuit, 1984.
Pierre Bourdieu, « La force du droit. Éléments pour une sociologie du champ juridique », Actes de la recherche en sciences sociales, n° 64, 1986, p. 5-19.
Pierre Bourdieu, La Noblesse d’État. Grandes écoles et esprit de corps, Paris, Éditions de Minuit, 1989.
Pierre Bourdieu, Les Règles de l’art. Genèse et structure du champ littéraire, Paris, Le Seuil, 1992.
Pierre Bourdieu, Les Structures sociales de l’économie, Paris, Le Seuil, 2000.
Pierre Bourdieu, « Une révolution conservatrice dans l’édition », Actes de la recherche en sciences sociales, n° 126/127, 1999, p. 3-28.
Pierre Bourdieu, Raisons pratiques. Sur la théorie de l’action, Paris, Le Seuil, 1994.
Pierre Bourdieu, Sur la télévision suivi de « L’emprise du journalisme », Paris, Raisons d’agir, 1996.
Pierre Bourdieu, Jean-Claude Chamboredon, Jean-Claude Passeron, Le Métier de sociologue [1967], Berlin-New York, Mouton de Gruyter, 2005 [5e édition], p. xiii-xiv.
Pierre Bourdieu, Rosine Christin, « La construction du marché. Le champ administratif et la production de la “politique du logement” », Actes de la recherche en sciences sociales, n° 81/82, 1990, p. 65-85.
Pierre Bourdieu, Monique de Saint Martin, « Anatomie du goût », Actes de la recherche en sciences sociales, n° 5, 1976, p. 3-81.
Pierre Bourdieu, Monique de Saint Martin, « Le patronat », Actes de la recherche en sciences sociales, n° 20/21, 1978, p. 3-82.
Pierre Bourdieu, Monique de Saint Martin, « La sainte famille. L'épiscopat français dans le champ du pouvoir », Actes de la recherche en sciences sociales, n° 44/45, 1982, p. 2-53.
Jean-Pierre Courtial, « À propos de l'analyse des données. Pour un dialogue entre méthodologue et chercheur », Revue française de sociologie, vol. 19, n° 4, 1978.
Alain Desrosières, « Analyse des données et sciences humaines : comment cartographier le monde social ? », Electronic Journ@l for History of Probability and Statistics, vol. 4, n° 2, 2008.
Julien Duval, « L'analyse des correspondances et la construction des champs », Actes de la recherche en sciences sociales, n° 200, 2013, p. 110-123.
Julien Duval, « Multiple Correspondence Analysis », in David Inglis, Anna-Mari Almila (dir.), The SAGE Handbook of Cultural Sociology, London, SAGE, 2016, p. 255-271.
Johannes Hjellbrekke, Olav Korsnes, « Quantifying the Field of Power in Norway », in Karen Robson, Chris Sanders (dir.) Quantifying Theory. Pierre Bourdieu, Toronto, Springer Netherlands, 2009, p. 31–46.
Ludovic Lebart, Marie Piron, Alain Morineau, Statistique exploratoire multidimensionnelle. Visualisation et inférence en fouille de données, Paris, Dunod, 2006 [4e édition].
John Levi Martin, « What is field theory? », American Journal of Sociology, vol. 109, n° 1, 2003, p. 1-49.
Brigitte Le Roux, Analyse géométrique des données multidimensionnelles, Paris, Dunod, 2014.
Brigitte Le Roux, Henry Rouanet, Geometric Data Analysis, Dordrecht, Kluwer, 2004.
Brigitte Le Roux, Henry Rouanet, Multiple Correspondence Analysis, Thousand Oaks, Sage, 2010.
Ece Kumbasar, Rommey A. Kimball, William H. Batchelder, « Systematic Biases in Social Perception », American Journal of Sociology, vol. 100, n° 2, 1994, p. 477-505.
David R. Gibson, « Taking Turns and Talking Ties : Networks and Conversational Interaction », American Journal of Sociology, vol. 110, n° 6, 2005, p. 1561-1597.
Virgilio Borges Pereira, Classes e Culturas de Classe das Famílias Portuenses. Classes sociais e «modalidades de estilização da vida» na cidade do Porto, Porto, Afrontamento/Instituto de Sociologia da Faculdade de Letras da Universidade do Porto, 2005.
Annick Prieur, Lennart Rosenlund, Jacob Skjott-Larsen, « Cultural capital today : a case study from Denmark », Poetics, vol. 36, n° 1, 2008, p. 45-71.
Lennart Roselund, « Cultural change in Norway: cultural and economic dimensions », International Journal of Contemporary Sociology, vol. 37, n° 2, 2000, p. 245-275.
Henry Rouanet, Werner Ackermann, Brigitte Le Roux, « The lesson of Bourdieu’s La Distinction », Bulletin de méthodologie sociologique, n° 65, 2000, p. 5-18.
Michèle Salitot-Dion, « Rôle du mariage dans l'accumulation des patrimoines chez les agriculteurs », Revue française de sociologie, vol. 16, n° 1, 1975, p. 59-78.
Gisèle Sapiro, « La raison littéraire. Le champ littéraire français sous l'Occupation (1940-1944) », Actes de la recherche en sciences sociales, n° 111, 1996, p. 3-35.
Gisèle Sapiro, La Guerre des écrivains, Paris, Fayard, 1999.
Lucie Tanguy, « L'État et l'école. L'école privée en France », Revue française de sociologie, vol. 13, n° 3, 1972, p. 325-375.
Karl Van Meter, Marie-Ange Schiltz, Philippe Cibois, Lise Mounier, « History and French Sociological Perspective », in M. Greenacre, J. Blasius (dir.), Correspondence Analysis in the Social Sciences, Londres, Academic Press, 1994, p. 128-137.









